PointInTriangle

计算机图形图像

I. Introduction

本文内容是如何判断一个点是否在指定三角形内。主要介绍了两种方式（原文实现为Java applet）。文章的描述针对的是二维的案例。

简而言之，问题的描述为：现给出三角形T,其三个顶点为V1= (vx1, vy1), V2= (vx2, vy2), V3= (vx3, vy3) 和测试点P = (px，py)。

问题：如何判断P是否包含在T中？

II. Algorithm 1: “Crossproduct Side Algorithm”

注意，上面这个算法的名称不是官方的，而是原文作者自己发明的（希望你们喜欢这个德国哥们取得这个名字！）。 请注意，以下主题和我在另外一篇文章中关于多边形凸性[1]的问题非常类似，但是在这里我们可以从另外一个角度看看这个问题。

也许你现在问自己如何在2D中定义 Crossproduct(叉乘？) 以及如何在几何上解释它？ 其实对于2D的情况，Crossproduct 实际上没有很好地定义，但是通常的定义如下：

1
perpDotProduct(v1, v2) = vx1 * vy2 - vy1 * vx2

这也被称为’perp dot’ 乘积，并且有很多有趣的属性 。如果您有兴趣，请阅读引用[2]。 有一点需要注意的是它返回标量而不是矢量（与3D叉乘相反），并且它与两个二元矢量的行列式相同。 从后面这点来看，显而易见（我的意思是一个优秀的数学家）可以得到以下有用的信息：

1
2
3
perpDotProduct(v1, v2) = 0   => v1, v2 平行
perpDotProduct(v1, v2) > 0   => v2 is clockwise from v1
perpDotProduct(v1, v2) < 0   => v1 is counterclockwise from v2

perpDotProduct的几何意义如下图所示。

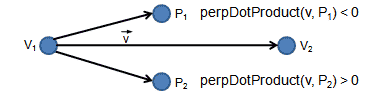
perpDotProductVisual.png

以上就是我们所需要的算法核心:)。用测试点P计算所有三个点V1，V2，V3 的 perpDotProduct / crossproduct。（此处请注意，在实际的三次计算中，P作为参数的位置需要保持不变。需要作为第一个或者第二个参数，否则在下面的检测算法中你可能会遇到麻烦！）。
计算
c1 = crossproduct(V1, P),
c2 = crossproduct(V2, P),
c3 = crossproduct(V3, P)。

最终点是否包含在三角形当中，取决于三角形相关的先验知识：

  • 若点 V1, V2, V3 是按照顺时针排列的，并且满足c1 > 0 && c2 > 0 && c3 > 0 为真,那么点P在三角形内。

  • 若点 V1, V2, V3 是按照逆时针排列的，并且满足c1 < 0 && c2 < 0 && c3 < 0 为真,那么点P在三角形内。

  • 若点 V1, V2, V3 的顺序未知，并且满足(c1> 0 && c2> 0 && c3 > 0) || (c1< 0 && c2< 0 && c3 < 0)为真,那么点P在三角形内。

III. Algorithm 2: “Barycentric Algorithm”

重心法是另外一个判断点是否包含在三角形内的算法。因为三角形是一个平面，所以它的所有顶点都在这个平面内。现在选择三角形的其中一个顶点以及包含这个点的两条边，从他们开始整个算法:

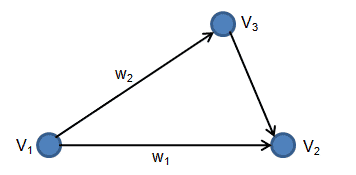
triangleplane.png

  • 定义w1 = V2-V1和w2 = V3-V1。
    然后包含在三角形平面中的每个点都可以写成：
    P（s，t）= V1 + s * w1 + t * w2 [定义域 R].

  • 通过限制s和t
    s >= 0，t >= 0且（s + t）<= 1，
    然后函数 P（s，t）可以表示为三角形内的点！(也就是说这个函数的值域为三角形内的点)

因此，只要选择合适的s和t的值，通过满足三个限制 s >= 0，t >= 0 和（s + t）<= 1，函数P（s，t）可以表示三角形内部的任意点。

这意味着对于我们的测试点P而言，我们可以用这个函数P（s，t）来描述它，并且需要s和t满足P在T内的条件。为了达到我们的目的：检测P是否包含在T内部。显然，我们的目标是计算合适s和t的值，用来表示测试点P。

1
V1 + s * w1 + t * w2 = P

重新组织以上公式：

1
s * w1 + t * w2 = P - V1

或者使用向量的表达方式：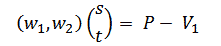
vectorNotation.png

现在我们可以手工解决这个问题，也可以应用克莱姆法则（Cramer’s Rule）[3]（但是对于我们现在的2D情况来说比较特殊，行列式的计算方法与perpDotProduct是相同的相同！）：

1
2
s = determinant(P - V1, V2) / determinant(V1, V2)
t = determinant(V1, P - V2) / determinant(V1, V2)

得到s,t 后若满足：
s >= 0 && t >= 0 && (s + t) <= 1 为真。那么即可判断点P位于三角形内。

希望这篇文章对大家有所帮助，如果有什么不理解的，可以看原文以及原文作者给出的applet源码，或者联系我。

引用
[1] Polygon Convexity
[2] The pleasures of “Perp Dot” Products by Hill in Graphics Gem IV on Google Books
[3] Cramer’s Rule @ Wikipedia

本文翻译自Sunshine 的 PointInTriangle

原文作者: Chaos

许可协议: 知识共享署名-非商业性使用 4.0 国际许可协议