RasterisingLinesCircles

计算机图形图像

1. Introduction

在这里本文向大家介绍下关于直线以及圆的光栅化的数学背景知识。虽然自己多多查询资料，多多编程实践，可以增强理解，但是本文的目的是向读者提供足够的信息以及动力去好好的理解算法(真的不是很理解原文作者的逻辑，哈哈)。光栅化直线和椭圆是计算机图形图像的基础算法，所以学习他们是很有必要的。因为网上已经有很多相关的文章，所以本文在这里不会描述所有的细节，但是本文会从最简单的算法入手，一步步深入扩展到其他算法，并且分析各个算法的优劣势，最终提出著名的Bresenham算法。本文的算法主要是关于直线和圆的，去掉了椭圆的部分。如果你理解了本文并且对绘制椭圆感兴趣的话，你可以查看引用[2]

2. Rasterizing Lines

我们假设直线的两个端点已经给定了，我们的目标就是去计算两个点的中间点。终点 P1 为(x1,y1),终点 P2 为(x2,y2).

2.1 Digital Differential Analyzer (DDA)

2.2 Bresenham Algorithm for Lines (Floating-point numbers)

2.3 Bresenham Algorithm for Lines (Integer numbers)

在 2.2章介绍的算法不足我们会在这章解决：

  • a) 该算法使用浮点数计算
  • b) 该算法只在第一象限有效

在2.2章的算法当中我们唯一的浮点数就是e, 为了解决问题a), 我们将误差值乘以 2 * dx。 现在我们定义: _e = 2 * dx * e并且替换掉2.2 章中的浮点数算法中每一个出现e的地方。
推导
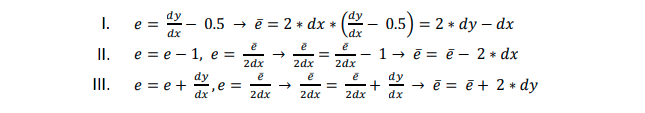
这个替换去除了所有的除法以及浮点数计算。
将这个算法应用到其他象限并不难：假设dy <= dx 代表x轴方向的长度大于y轴方向的长度，因为算法是沿着x轴方向扫描的。如果 dy > dx 那么我们使用一个额外变量的交换dy与dx。第二，线的方向必须被重新计算。在2.2章中我们假设y2 > y1 且 x2 > y1。在y1> y2的情况下，线的方向是向下而不是向上，所以我们必须减少y的值而不是增加y的值;这个过程同样适用于x。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
public void BresenhamInt(int x1, int y1, int x2, int y2)
{
    boolean changed;
    int x = x1;
    int y = y1;

    int dx = |x2 – x1|;
    int dy = |y2 – y1|;

    int signx = signum(x2 – x1);
    int signy = signum(y2 – y1);
    
    /* 2.2章的算法默认是在一个象限的算法满足dy < dx 即可 
     * 这里因为要考虑其他象限所以需要考虑dy > dx 的情况
     */
    if (dy > dx)
    {
        swap(dx, dy);
        changed = true;
    }

    /* 替换2.2 浮点数算法的逻辑
     * float e = ((float)dy/(float)dx);
     */ 
    float e = 2 * dy - dx;
    for (int i = 1; i <= dx; i++)
    {
        plot(x, y);
        while (e >= 0)
        {   
            //考虑不同情况下误差的累计
            if (changed)
                x = x + 1;
            else
                y = y + 1;

            /* 替换2.2 浮点数算法的逻辑
             * e = e – 1;
             */
            e = e – 2 * dx;
        }
        if (changed)
            y += signy;
        else
            x += signx;

        /* 替换2.2 浮点数算法的逻辑
         * e = e + (float)dy/(float)dx;
         */ 
        e = e + 2 * dy;
    }
}

3. Rasterizing Circles

与上两章一样，我们还是从一个不是很完美的算法开始 一步一步的深入扩展到一个非常好的算法。
在这里我们通过一个点 midpoint (mx, my) 以及一个半径r定义一个圆。

3.1 Simple approach evaluating the circle equation

光栅化一个圆最简单的算法是基于圆的方程。
(x - mx)2 + (y-my)2 = r2

该方程的解为：
y = my ± √r2 - (x-mx)2

这个等式也揭示了圆的对称性质。因为±的存在，我们可以看出，每一个x对应着两个y值，一个在原点的上面，一个再原点的下面。
如下图Figure 4所示：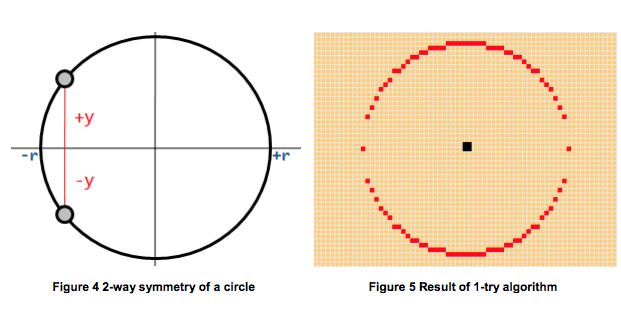
symmetry of a circle
基于以上事实，我们很容易想到在一个在x方向上从-r到+r的逐像素算法，每个x的值计算两个y的值，并且绘制这两个点。

1
2
3
4
5
6
for (x = -radius; x <= radius; x++)
{
    fy = sqrt( (radius*radius) – x*x);
    plot(mx + x, my + fy); // 绘制原点上的点
    plot(mx + x, my – fy); // 绘制原点下的点
}

不幸的是，如果你实现并且验证了这个算法的话，你会看到圆圈上面的洞，如上图Figure 5 所示。其实在2.2章中我们也会遇到这个问题，但是我们通过限制了线条的斜率小于45度规避了问题。在这里我们可以看见，如果斜率过大就会出现洞，因为当前点与下一个点之间的y的差值大于x之间的差值。当然了我们可以沿用之间的解决方案，检查每一个步骤当前的斜率，然后根据斜率决定我们该沿着x轴方向还是y轴方向。

一个更加优雅的解决方案就是利用圆的对称性。通过计算圆上的一个点，利用圆的对称性实际能得到8个计算好的点。如图见下图Figure 6: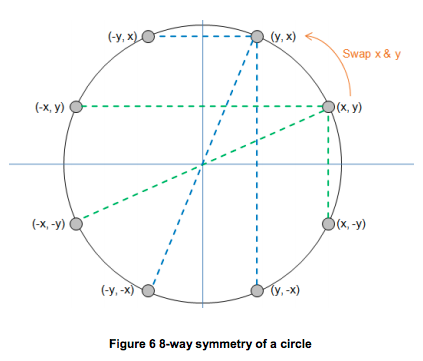
symmetry of a circle
利用这种8向对称性，最终可以绘制出正确的圆。
Using this 8-way symmetry, a correct circle can finally be drawn. Instead of proceeding the range [-radius, radius] in the loop, it’s enough to go from 1 to the point where y becomes greater than x (the point where the slope get’s so big that holes occur) and get the other points by symmetry. The pseudo code is given in xxx, again we add 0.5 to get the correct rounding values (not that y is a double, but for plotting a pixel it’s casted to an integer):这段很难翻译，暂时放在这里
然后通过圆的对称性得到其他点。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public void CircleSimple(int mx, int my, int radius)
{
    double y;
    int x = 1;
    y = sqrt((radius*radius) – (x*x)) + 0.5;
    while (x <= y)
    {
        plot(mx + x, my + y);
        plot(mx + x, my - y);
        plot(mx - x, my + y);
        plot(mx - x, my - y);
        plot(mx + y, my + x);
        plot(mx + y, my - x);
        plot(mx - y, my + x);
        plot(mx - y, my - x);
        x += 1;
        y = sqrt((radius*radius) – (x*x)) + 0.5;
    }
}

3.2 Bresenham for Circles (floating point numbers)

虽然结果看起来不错，现在我们试着去优化一下它。 在以上算法中，开平方根计算出现在每一次循环当中，它的计算是非常密集的。所以现在我们的目的是寻找计算速度更快，绘制效果更好的增量算法。下面就让我们来用这个简化的，坐标原点midpoint为（0，0）的圆方程x2 + y2 = r2，一步一步来分析，实现这个算法。
这个圆方程，可以通过将它平移到任意点，推广到更加一般的情况。通过上面的例子，我们知道可以通过绘制一个点，然后利用圆的对称性绘制其他象限的点，所以在这里我们先考虑第一象限的情况。

首先让我们来看看这个圆的隐函数，F(x,y) = x2 + y2 - r2,在圆上的点都满足F(x,y) = 0;在圆内的点都满足F(x,y) < 0;在圆外的点都满足F(x,y) > 0;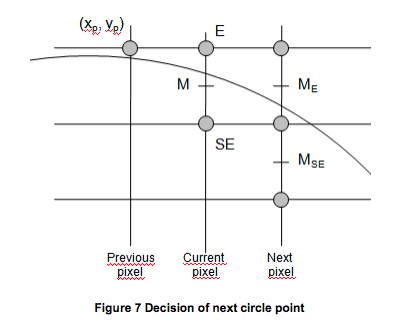
7 Decision of next circle point

假设当前点为（Xp,Yp）如上图Figure 7 所示。至于下一个点到底取E还是SE取决于M和圆的相对关系，也就是F(M)的符号。现在我们先创建一个决策变量dold。
dold = F(M) = F(Xp + 1,Yp - 1/2) = (Xp + 1)2 + (Yp - 1/2)2 - R2
如果 dold < 0。那么M就是在圆里面，

3.3 Bresenham for Circles (integer numbers)

4. References

[1]wikipedia DDA)
[2]bcircle
[3]University of Karlsruhe, Einführung in die graphische Datenverarbeitung

本文翻译自Sunshine 的 RasterisingLinesCircles

原文作者: Chaos

许可协议: 知识共享署名-非商业性使用 4.0 国际许可协议